Ch 2 Limits and Continuity Calculus

Lecture 2 Ch 2. Limits and Continuity Calculus I Iksan Bukhori, M. Phil iksan. [email protected] ac. id 2019

Textbook and Syllabus Textbook: "Thomas' Calculus", George B. Thomas, Jr. Pearson, 13 th Edition, 2013. Syllabus: (tentative) Chapter 1: Functions Chapter 2: Limits and Continuity Chapter 3: Derivatives Chapter 4: Applications of Derivatives Chapter 5: Integrals Iksan Bukhori Calculus I 1/2

Grade Policy Grade Point: 85 – 100 70 – 84 60 – 69 55 – 59 0 – 54 : A : B : C : D : E (GPA = 4) (GPA = 3) (GPA = 2) (GPA = 1) (GPA = 0) § The use of smartphone calculator in quizzes and exams is prohibited. Iksan Bukhori Calculus I 1/3

Grade Policy Grades: Final Grade = 10% Homeworks + 20% Quizzes + 30% Midterm Exam + 40% Final Exam + Extra Points § Homeworks will be given in fairly regular basis. The average of homework grades contributes 10% of final grade. § Homeworks are to be written on A 4 papers, otherwise they will not be graded. § Homeworks must be submitted on time, on the schedule of the lecture. If you submit late, the penalty will be – 10·n points, where n is the total number of lateness made. § There will be 2 quizzes The average of quiz grades contributes 20% of final grade. § Midterm and final exam schedule will be announced in time. Iksan Bukhori Calculus I 1/4

Grade Policy § Extra points will be given if you solve a problem in front of the class. You will earn 1, 2, or 3 points. § Make up of quizzes and exams will be held within one week after the schedule of the respective quizzes and exams. § To maintain the integrity, the maximum score of a make up quiz or exam can be set to 90. Basic Physics 1 Homework 6 Rudi Bravo 009201700008 21 March 2021 No. 1. Answer: . . . . Heading of Homework Papers (Required) Iksan Bukhori Calculus I 1/5

Lecture Activities § Lectures will be held in the form of Power. Point presentations. § You are expected to write a note along the lectures to record your own conclusions or materials which are not covered by the lecture slides. How to get good grades in this class? • Do the homeworks by yourself • Solve problems in front of the class • Take time to learn at home • Ask questions Iksan Bukhori Calculus I 1/6

Lecture Material § Latest lecture slides will be uploaded to my blog [email protected] com § You are responsible to read and understand the lecture slides. I am responsible to answer your questions. § Quizzes, midterm exam, and final exam will be open-cheat sheets. Be sure to have your own copy of lecture slides. You are not allowed to borrow or lend anything during quizzes or exams. § But: A homework can be submitted late without penalty if a scanned or photographed version of the homework is sent to iksan. [email protected] ac. id at least one day before the schedule of the class. Iksan Bukhori Calculus I 1/7

Extra Assignments § There will be no remedial for any quizzes nor exams. § As replacement, you may submit a neat summary of your notes or collection of problems and solutions related to all topics covered up to that point in handwritten with A 4 paper § This extra assignment will not be announced beforehand has to be submitted one day after your quiz/exams paper is returned § The extra grade depends on the materials covered, how neat it is and how good your understanding of the materials actually is (Copying my slides or the book(s) will not do) Iksan Bukhori Calculus I 1/8

2. 1 Rates of Change and Limits Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Average Rates of change and Secant Lines q Given an arbitrary function y=f(x), we calculate the average rate of change of y with respect to x over the interval [x 1, x 2] by dividing the change in the value of y, Dy, by the length Dx Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 10
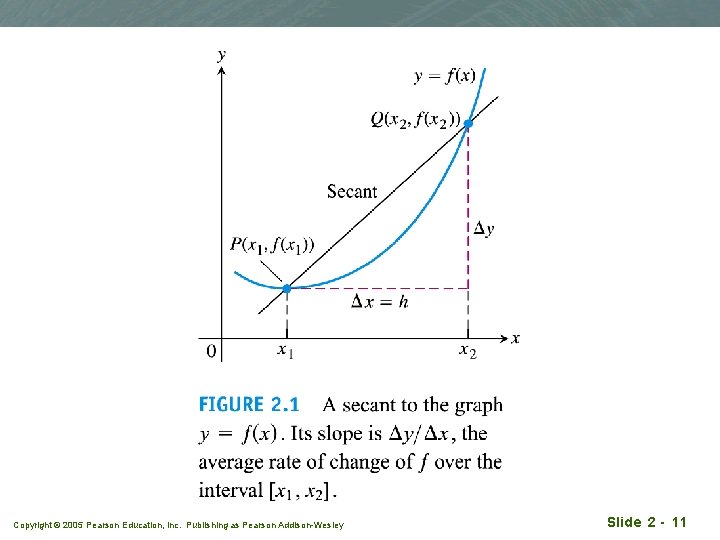
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 11

Example 4 q Figure 2. 2 shows how a population of fruit flies grew in a 50 -day experiment. q (a) Find the average growth rate from day 23 to day 45. q (b) How fast was the number of the flies growing on day 23? Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 12
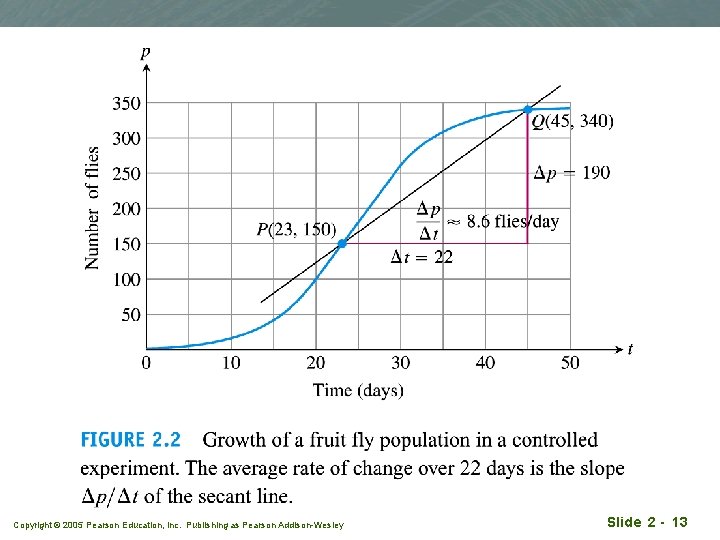
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 13
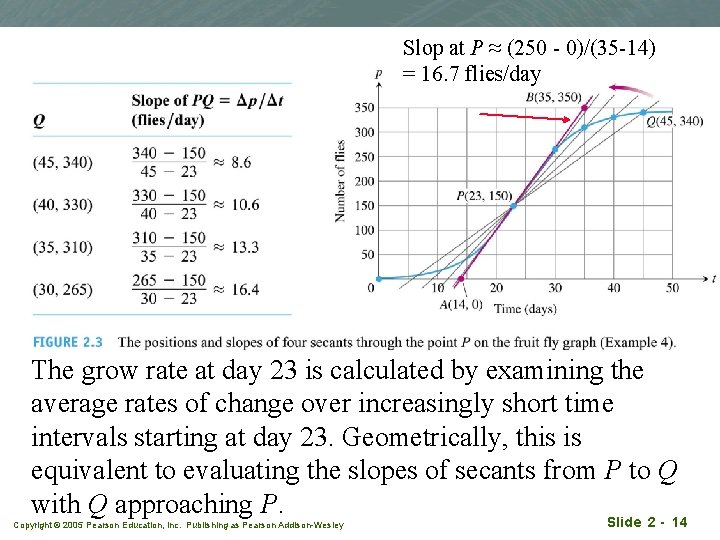
Slop at P ≈ (250 - 0)/(35 -14) = 16. 7 flies/day The grow rate at day 23 is calculated by examining the average rates of change over increasingly short time intervals starting at day 23. Geometrically, this is equivalent to evaluating the slopes of secants from P to Q with Q approaching P. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 14

Limits of function values q Informal definition of limit: q Let f be a function defined on an open interval about x 0, except possibly at x 0 itself. q If f gets arbitrarily close to L for all x sufficiently close to x 0, we say that f approaches the limit L as x approaches x 0 q "Arbitrarily close" is not yet defined here (hence the definition is informal). Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 15

Example 5 q How does the function behave near x=1? q Solution: Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 16

We say that f(x) approaches the limit 2 as x approaches 1, Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 17
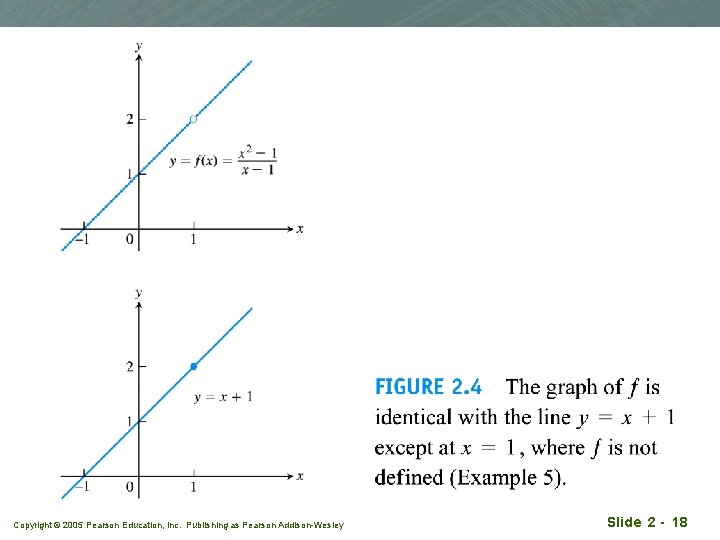
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 18
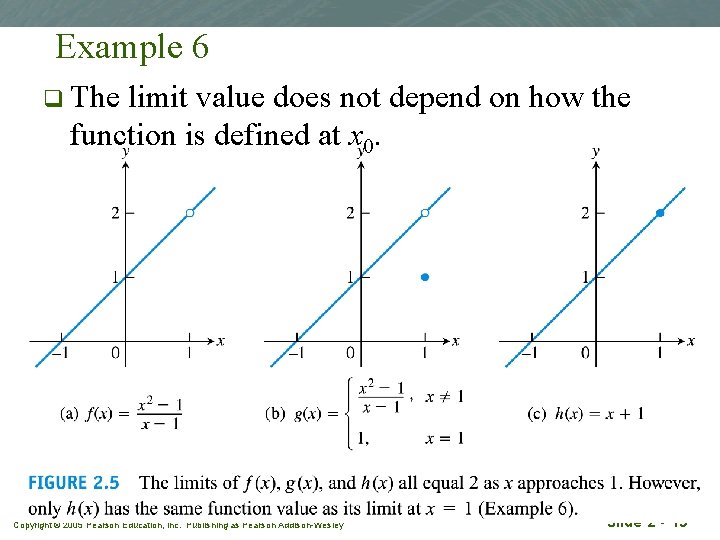
Example 6 q The limit value does not depend on how the function is defined at x 0. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 19

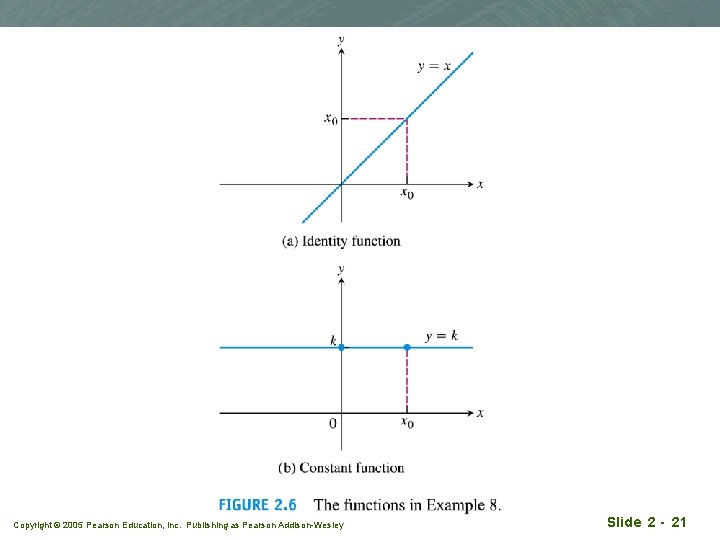
Example 7 q q q In some special cases limx→x 0 f(x) can be evaluated by calculating f (x 0). For example, constant function, rational function and identity function for which x=x 0 is defined (a) limx→ 2 (4) = 4 (constant function) (b) limx→-13 (4) = 4 (constant function) (c) limx→ 3 x = 3 (identity function) (d) limx→ 2 (5 x-3) = 10 – 3 =7 (polynomial function of degree 1) (e) limx→ -2 (3 x+4)/(x+5) = (-6+4)/(-2+5) =-2/3 (rational function) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 20
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 21
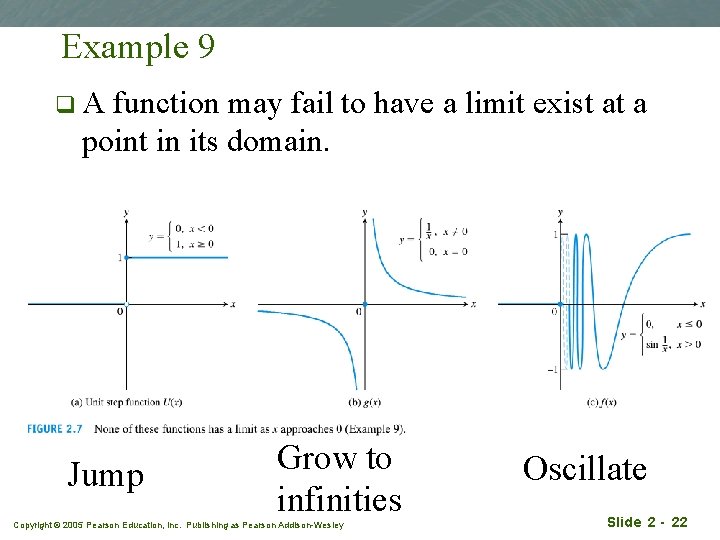
Example 9 q. A function may fail to have a limit exist at a point in its domain. Jump Grow to infinities Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Oscillate Slide 2 - 22

2. 2 Calculating limits using the limits laws Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

The limit laws q Theorem 1 tells how to calculate limits of functions that are arithmetic combinations of functions whose limit are already known. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 24

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 25

Example 1 Using the limit laws q (a) limx→ c (x 3+4 x 2 -3) = limx→ c x 3 + limx→ c 4 x 2 - limx→ c 3 (sum and difference rule) = c 3 + 4 c 2 - 3 (product and multiple rules) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 26

Example 1 q (b) limx→ c (x 4+x 2 -1)/(x 2+5) = limx→ c (x 4+x 2 -1) /limx→ c (x 2+5) =(limx→c x 4 + limx→cx 2 -limx→ c 1)/(limx→ cx 2 + limx→ c 5) = (c 4 +c 2 - 1)/(c 2 + 5) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 27

Example 1 q (c) limx→ -2 (4 x 2 -3) = limx→ -2 (4 x 2 -3) Power rule with r/s = ½ = [limx→ -2 4 x 2 - limx→ -2 3] = [4(-2)2 - 3] = 13 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 28

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 29

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 30

Example 2 q Limit of a rational function Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 31

Eliminating zero denominators algebraically Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 32

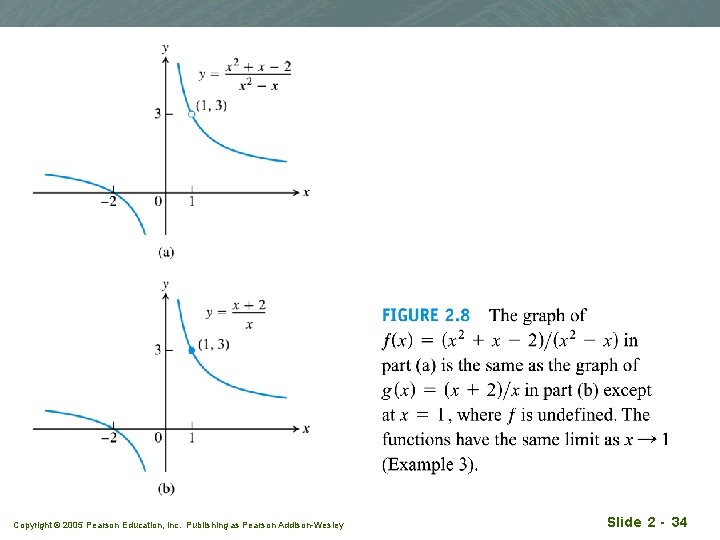
Example 3 Canceling a common factor q Evaluate q Solution: We can't substitute x=1 since f (x = 1) is not defined. Since x 1, we cancel the common factor of x-1: Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 33
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 34

The Sandwich theorem Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 35
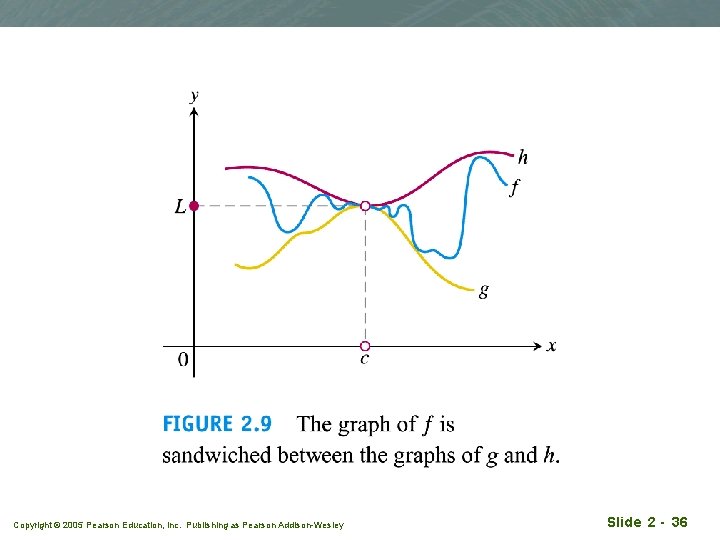
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 36

Example 6 (a) q The function y =sin q is sandwiched between y = |q | and y= -|q | for all values of q. Since limq→ 0 (|q |) = 0, we have limq→ 0 sin q = 0. q (b) q From the definition of cos q, 0 ≤ 1 - cos q ≤ |q | for all q, and we have the limit limx→ 0 cos q = 1 q Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 37
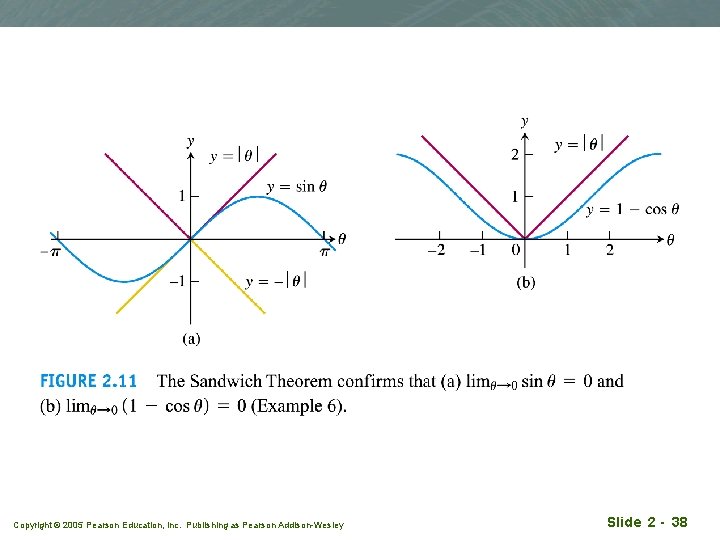
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 38

Example 6(c) any function f (x), if limx→ 0 (|f (x) |) = 0, then limx→ 0 f (x) = 0 due to the sandwich theorem. q Proof: -|f (x)| ≤ f (x) ≤ |f (x)|. q Since limx→ 0 (|f (x) |) = limx→ 0 (-|f (x) |) = 0 q limx→ 0 f (x) = 0 q For Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 39

Homework 2 q Slide 2 - 40

2. 3 The Precise Definition of a Limit Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Example 1 A linear function q Consider the linear function y = 2 x – 1 near x 0 = 4. Intuitively it is close to 7 when x is close to 4, so limx 0 (2 x-1)=7. How close does x have to be so that y = 2 x -1 differs from 7 by less than 2 units? Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 42
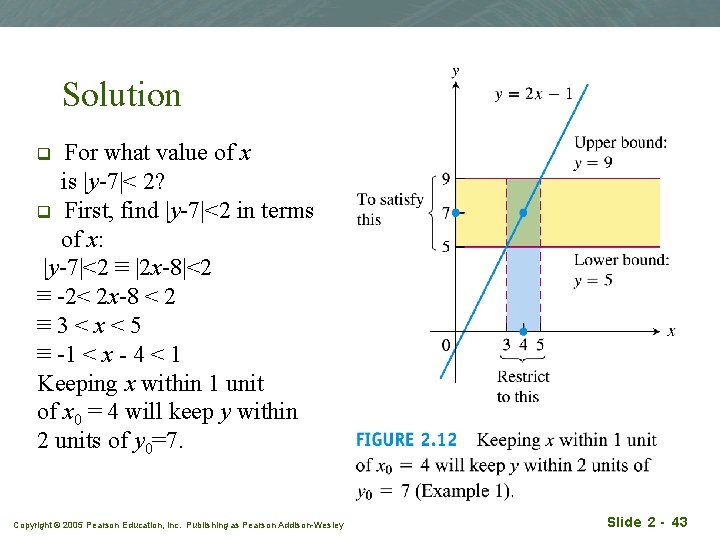
Solution For what value of x is |y-7|< 2? q First, find |y-7|<2 in terms of x: |y-7|<2 ≡ |2 x-8|<2 ≡ -2< 2 x-8 < 2 ≡ 3<x<5 ≡ -1 < x - 4 < 1 Keeping x within 1 unit of x 0 = 4 will keep y within 2 units of y 0=7. q Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 43

Definition of limit Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 44

Definition of limit Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 45

• The problem of proving L as the limit of f (x) as x approaches x 0 is a problem of proving the existence of d, such that whenever • x 0 – d < x< x 0+d, • L+e < f (x) < L-e for any arbitrarily small value of e. • As an example in Figure 2. 13, given e = 1/10, can we find a corresponding value of d ? • How about if e = 1/100? e = 1/1234? • If for any arbitrarily small value of e we can always find a corresponding value of d, then we has successfully proven that L is the limit of f as x approaches x 0 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 46
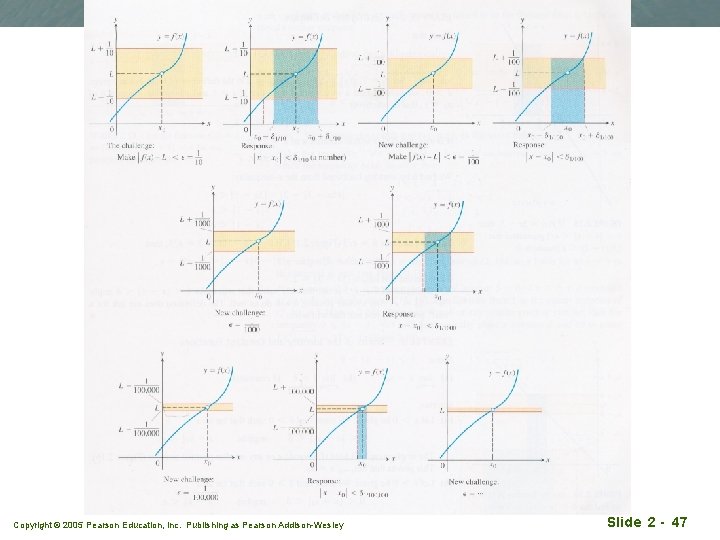
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 47
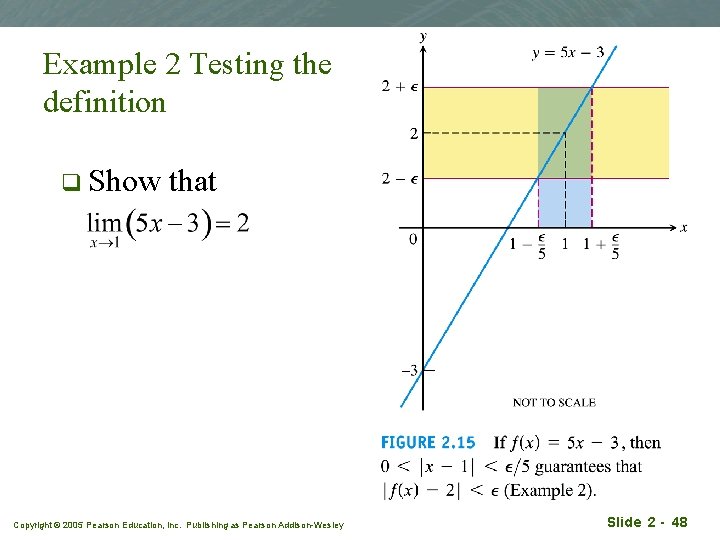
Example 2 Testing the definition q Show that Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 48
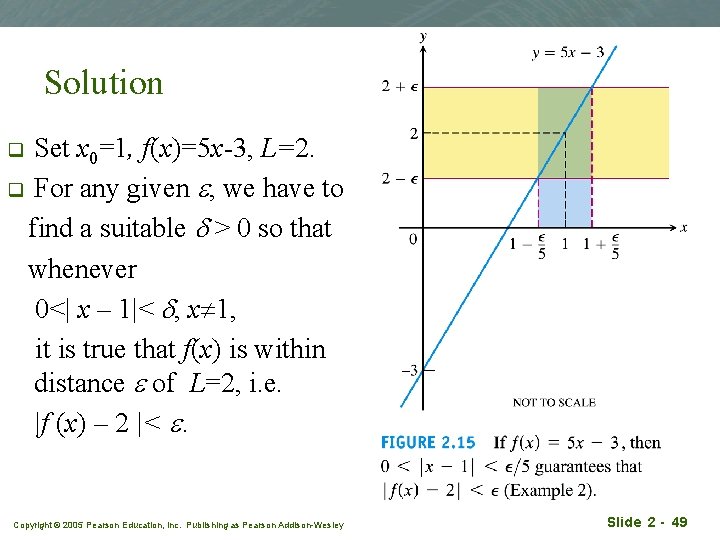
Solution Set x 0=1, f(x)=5 x-3, L=2. q For any given e, we have to find a suitable d > 0 so that whenever 0<| x – 1|< d, x 1, it is true that f(x) is within distance e of L=2, i. e. |f (x) – 2 |< e. q Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 49

q First, obtain an open interval (a, b) in which |f(x) 2|< e ≡ |5 x - 5|< e ≡ -e /5< x - 1< e /5 ≡ -e /5< x – x 0< e /5 a q ( x 0 -e /5 x 0 x ) x 0+ e /5 b choose d < e / 5. This choice will guarantee that |f(x) – L| < e whenever x 0–d < x 0 + d. We have shown that for any value of e given, we can always find an corresponding value of d that meets the "challenge" posed by an ever diminishing e. This is an proof of existence. Thus we have proven that the limit for f(x)=5 x-3 is L=2 when x x 0=1. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 50

Example 3(a) q Limits of the identity functions q Prove Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 51
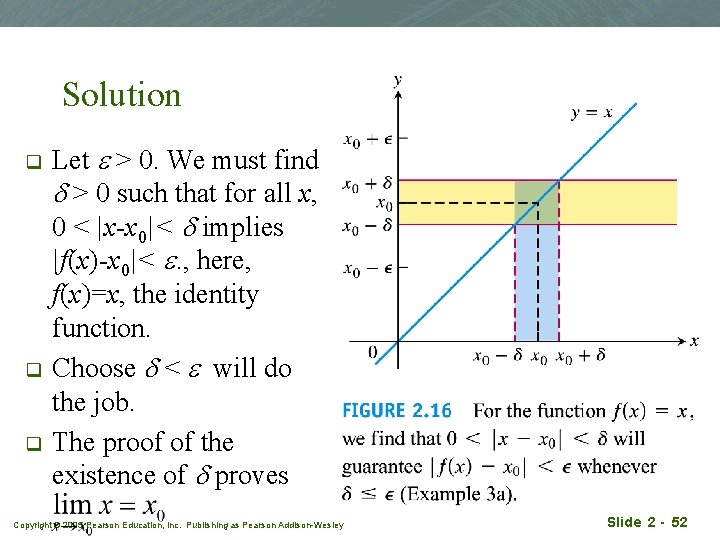
Solution q q q Let e > 0. We must find d > 0 such that for all x, 0 < |x-x 0|< d implies |f(x)-x 0|< e. , here, f(x)=x, the identity function. Choose d < e will do the job. The proof of the existence of d proves Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 52
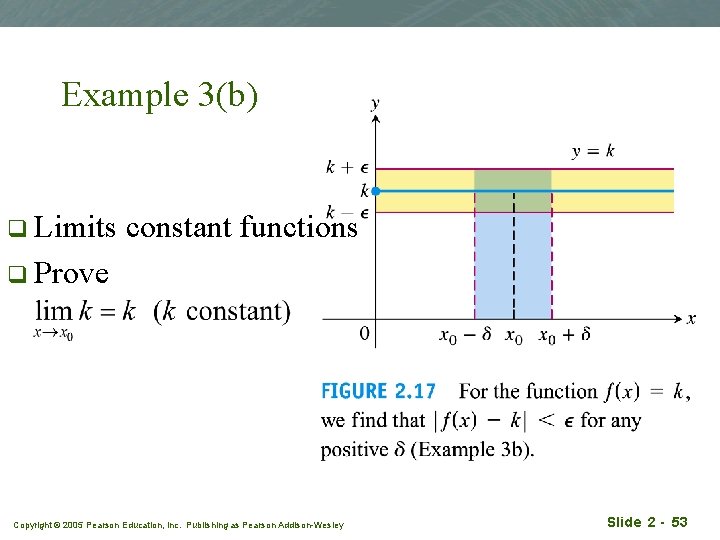
Example 3(b) q Limits constant functions q Prove Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 53
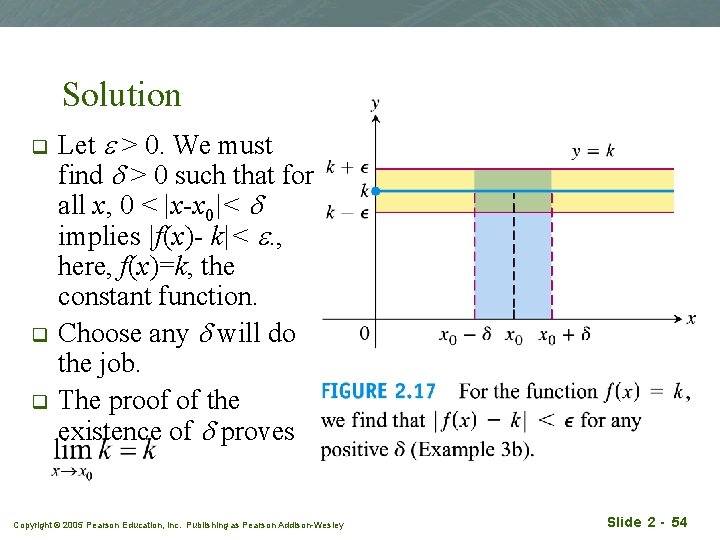
Solution q q q Let e > 0. We must find d > 0 such that for all x, 0 < |x-x 0|< d implies |f(x)- k|< e. , here, f(x)=k, the constant function. Choose any d will do the job. The proof of the existence of d proves Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 54

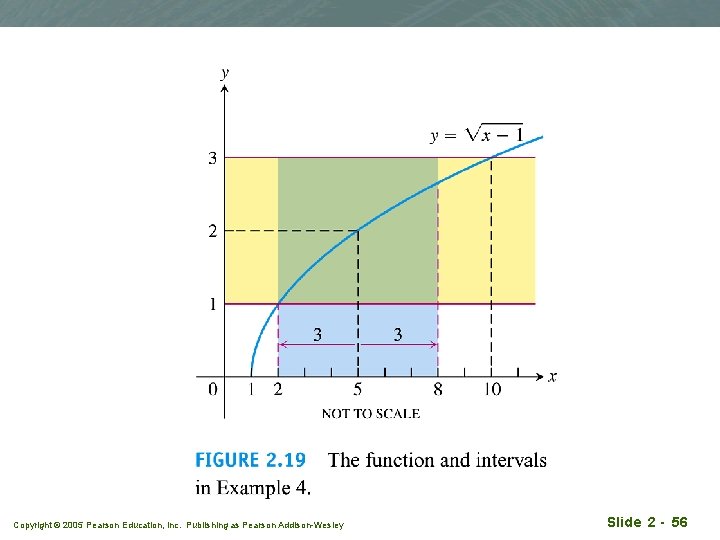
Finding delta algebraically for given epsilons q Example 4: Finding delta algebraically q For the limit find a d > 0 that works for e = 1. That is, find a d > 0 such that for all x, Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 55
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 56

Solution qd is found by working backward: Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 57

Solution q q Step one: Solve the inequality |f(x)-L|<e Step two: Find a value of d > 0 that places the open interval (x 0 -d, x 0+d ) centered at x 0 inside the open interval found in step one. Hence, we choose d = 3 or a smaller number x 0=5 By doing so, the inequality 0<|x - 5| < d will automatically place x between 2 and 10 to make d =3 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley d =3 Interval found in step 1 Slide 2 - 58
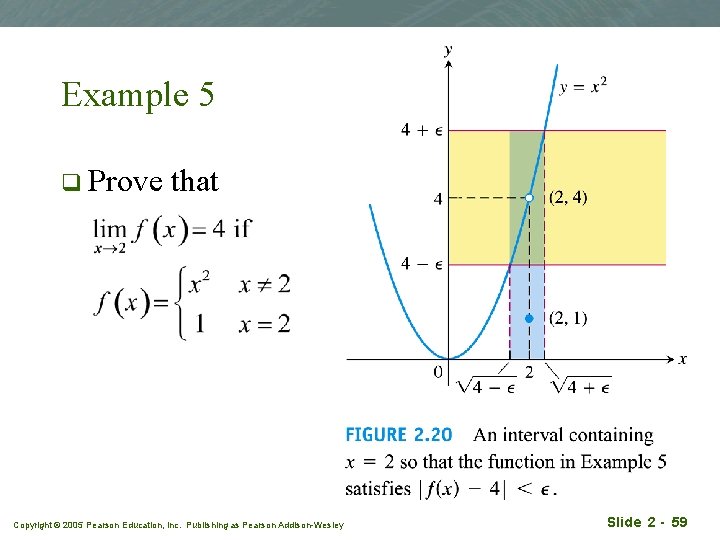
Example 5 q Prove that Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 59
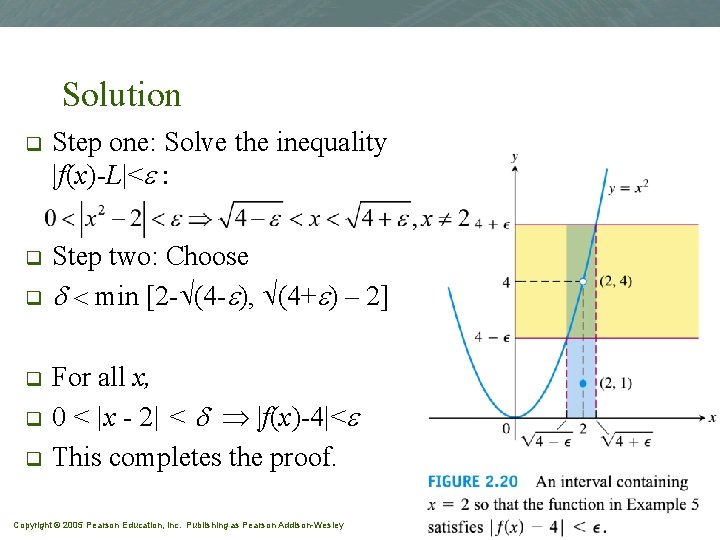
Solution q Step one: Solve the inequality |f(x)-L|<e : q Step two: Choose d < min [2 - (4 -e), (4+e) – 2] q q For all x, 0 < |x - 2| < d |f(x)-4|<e This completes the proof. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 60

2. 4 One-Sided Limits and Limits at Infinity Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Two sided limit does not exist for y; But y does has two onesided limits Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 62
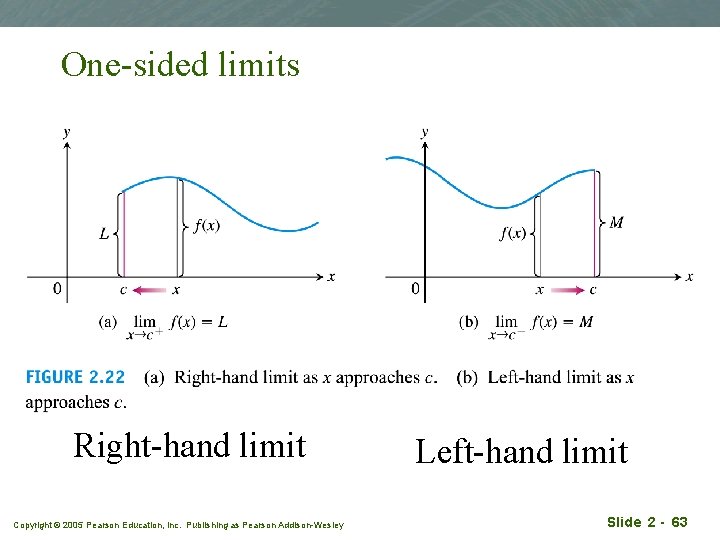
One-sided limits Right-hand limit Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Left-hand limit Slide 2 - 63

Example 1 q One sided limits of a semicircle No left hand limit at x= -2; No right hand limit at x=2; No two sided limit at x= 2; No two sided limit at x= -2; Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 64

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 65
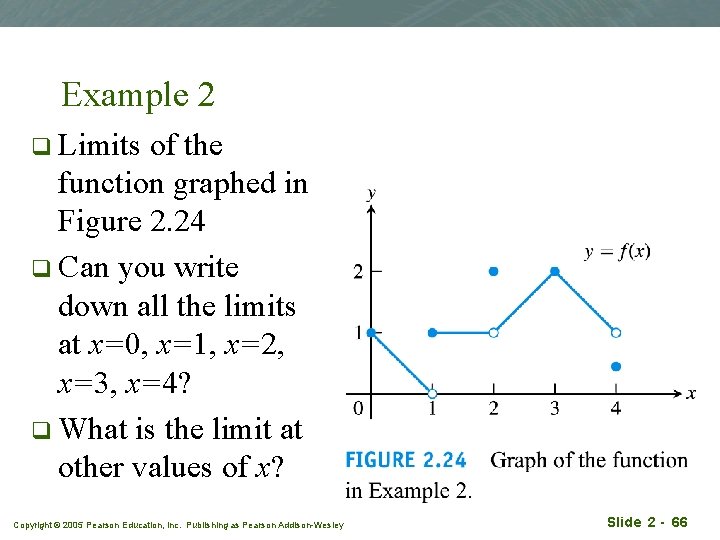
Example 2 q Limits of the function graphed in Figure 2. 24 q Can you write down all the limits at x=0, x=1, x=2, x=3, x=4? q What is the limit at other values of x? Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 66

Precise definition of one-sided limits Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 67
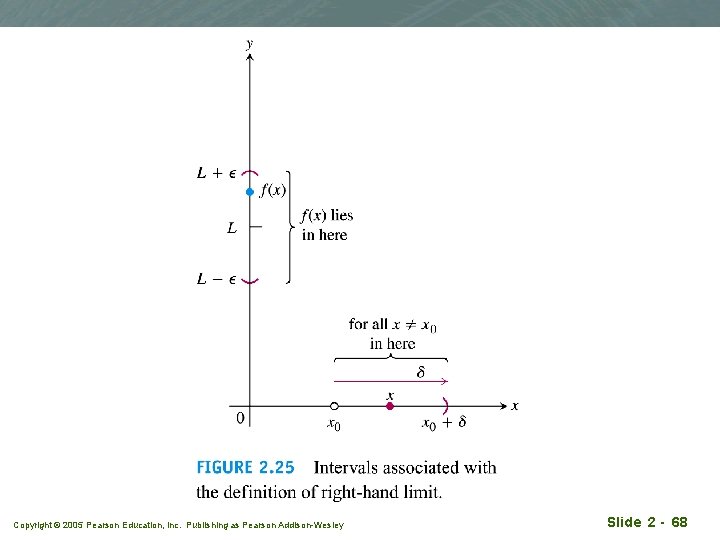
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 68
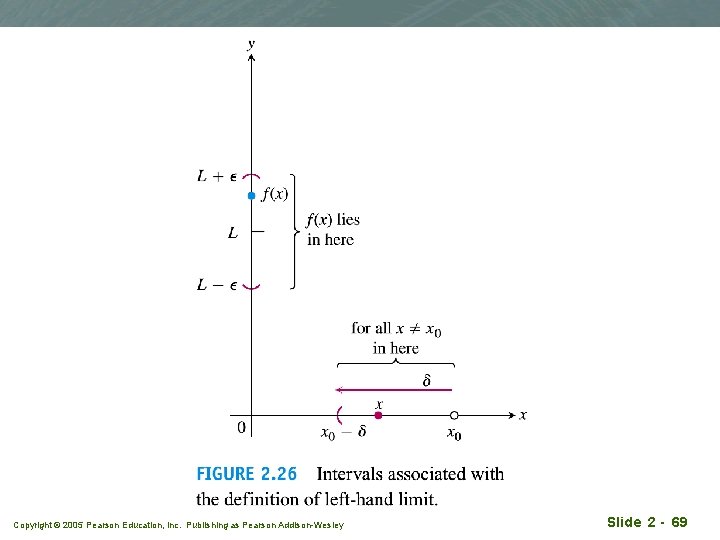
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 69
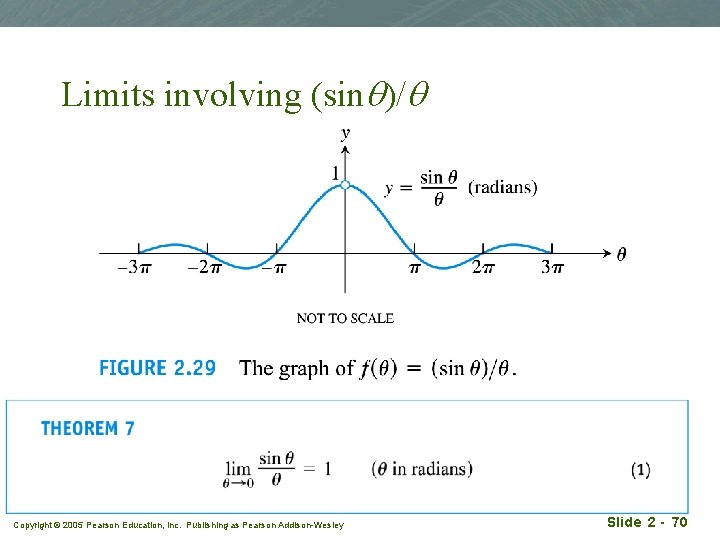
Limits involving (sinq)/q Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 70
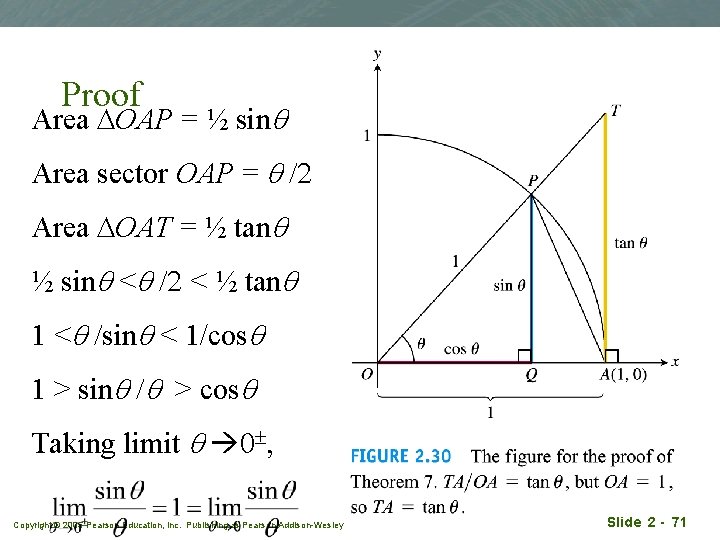
Proof Area DOAP = ½ sinq Area sector OAP = q /2 Area DOAT = ½ tanq ½ sinq <q /2 < ½ tanq 1 <q /sinq < 1/cosq 1 > sinq /q > cosq Taking limit q 0 , Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 71

Example 5(a) q Using theorem 7, show that Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 72

Example 5(b) q Using theorem 7, show that Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 73
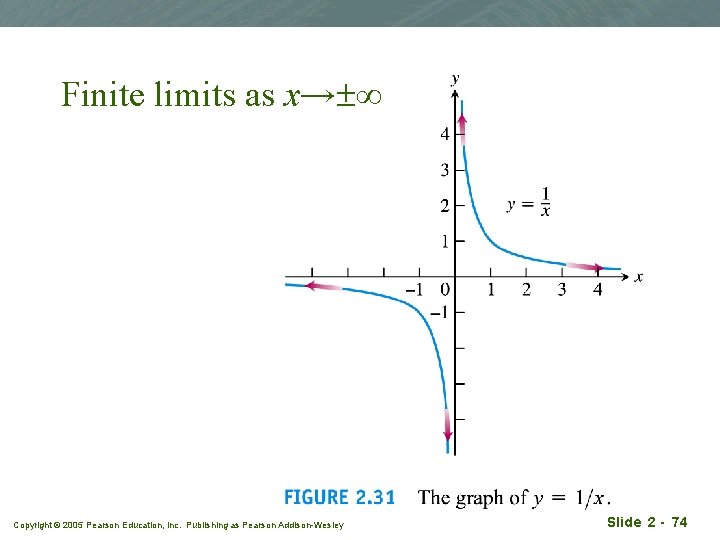
Finite limits as x→ ∞ Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 74

Precise definition Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 75

Example 6 q Limit at infinity for q (a) Show that q (b) Show that Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 76
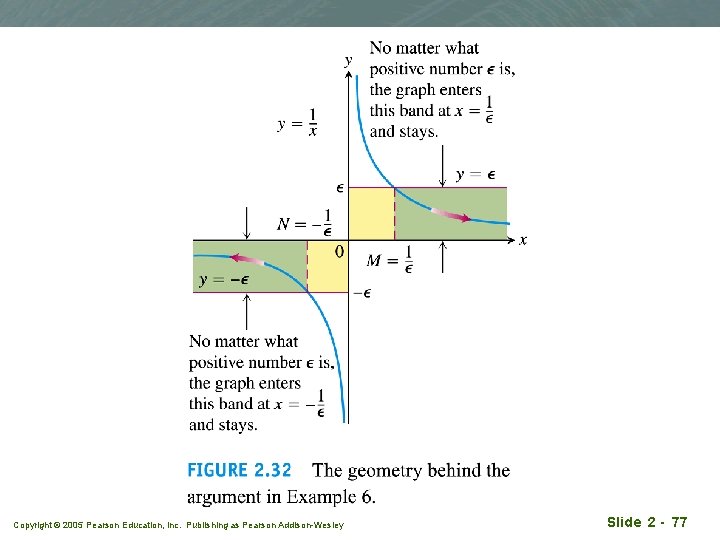
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 77

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 78

Example 7(a) q Using Theorem 8 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 79

Example 7(b) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 80

Limits at infinity of rational functions q Example 8 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 81
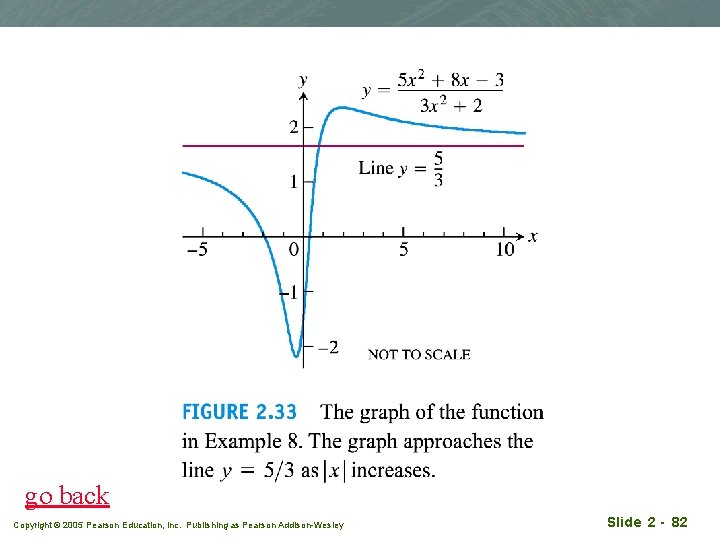
go back Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 82

Example 9 q Degree of numerator less than degree of denominator Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 83
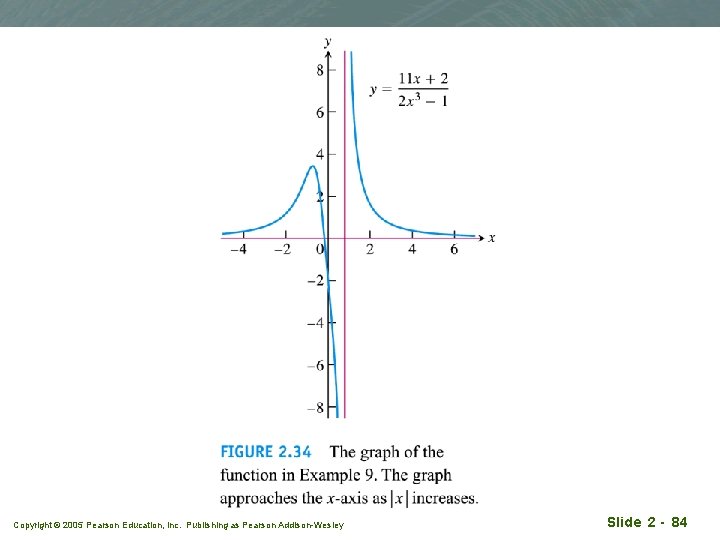
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 84
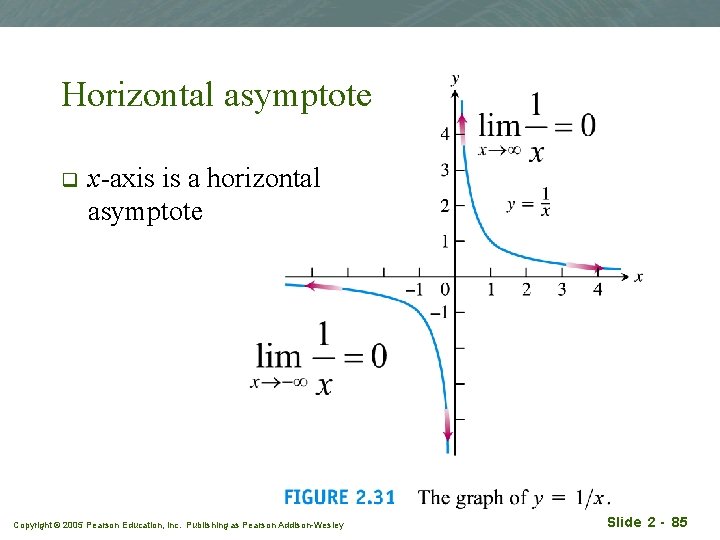
Horizontal asymptote q x-axis is a horizontal asymptote Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 85

Figure 2. 33 has the line y=5/3 as a horizontal asymptote on both the right and left because Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 86

Oblique asymptote q Happen when the degree of the numerator polynomial is one greater than the degree of the denominator q By long division, recast f (x) into a linear function plus a remainder. The remainder shall → 0 as x → ∞. The linear function is the asymptote of the graph. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 87
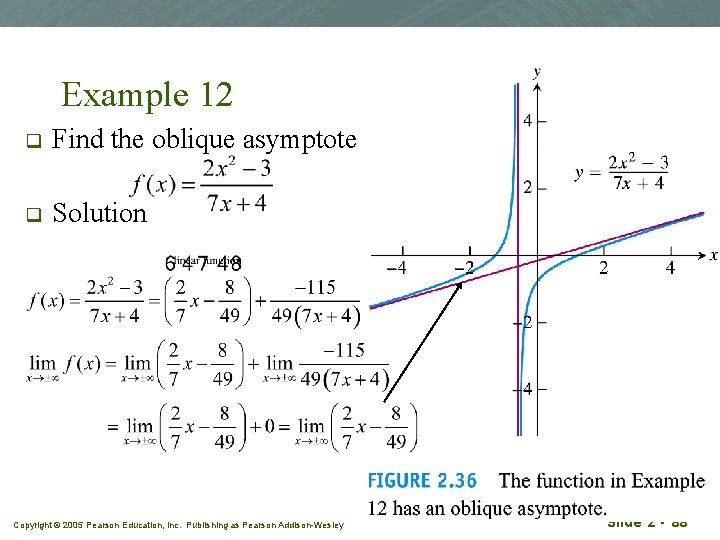
Example 12 q Find the oblique asymptote for q Solution Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 88

2. 5 Infinite Limits and Vertical Asymptotes Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
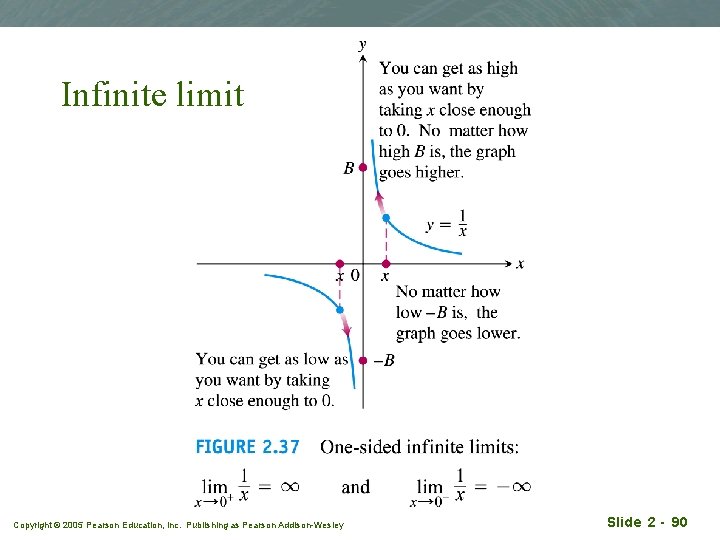
Infinite limit Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 90
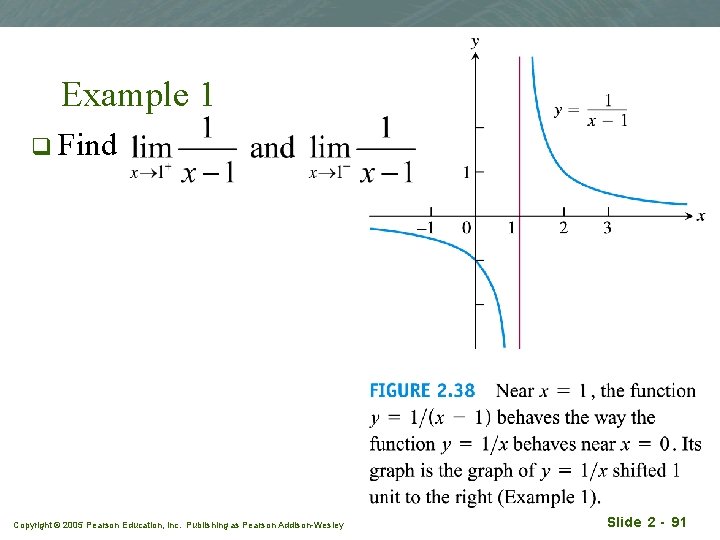
Example 1 q Find Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 91

Example 2 Two-sided infinite limit q Discuss the behavior of Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 92
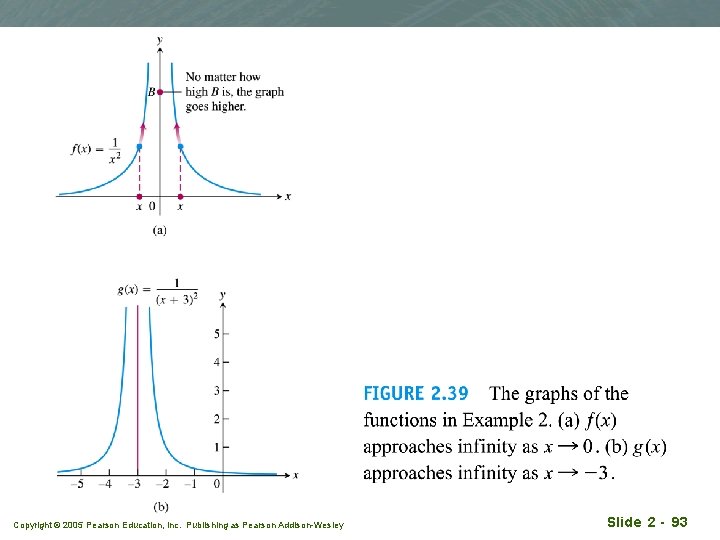
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 93

Example 3 q Rational functions can behave in various ways near zeros of their denominators Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 94

Example 3 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 95

Precise definition of infinite limits Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 96
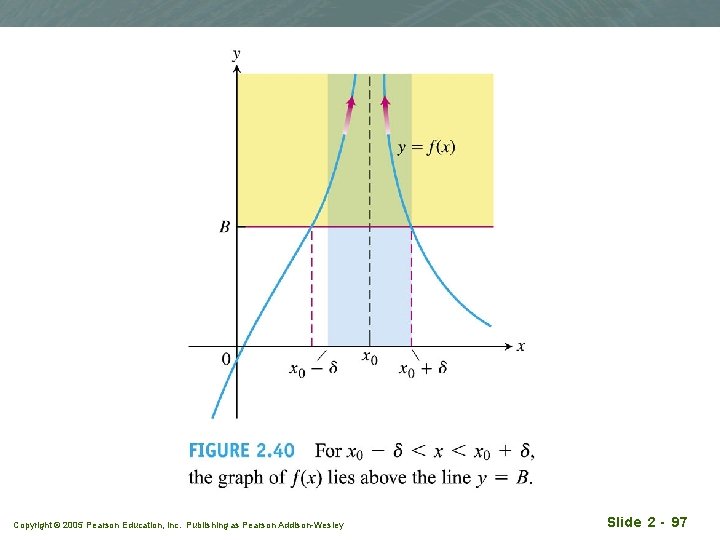
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 97
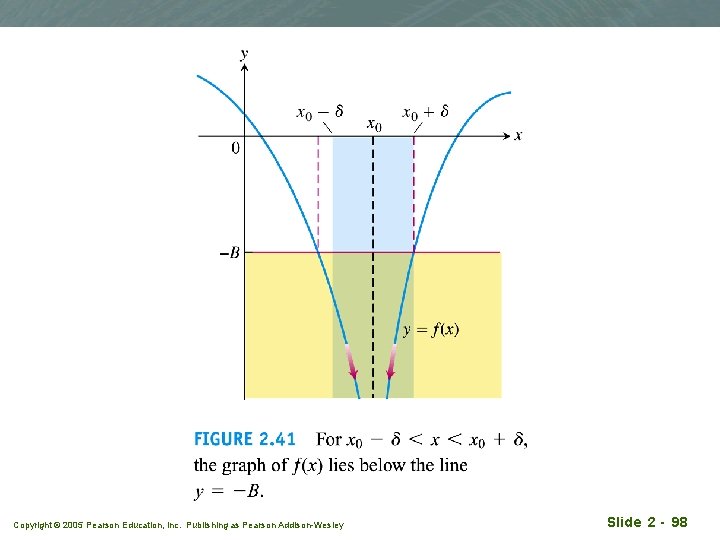
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 98

Example 4 q Using definition of infinite limit q Prove that Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 99

Example 4 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 100
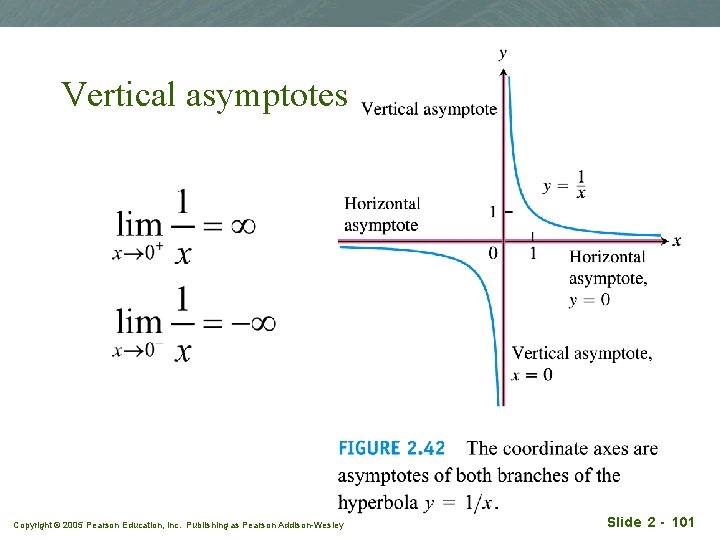
Vertical asymptotes Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 101

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 102

Example 5 Looking for asymptote q Find the horizontal and vertical asymptotes of the curve q Solution: Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 103
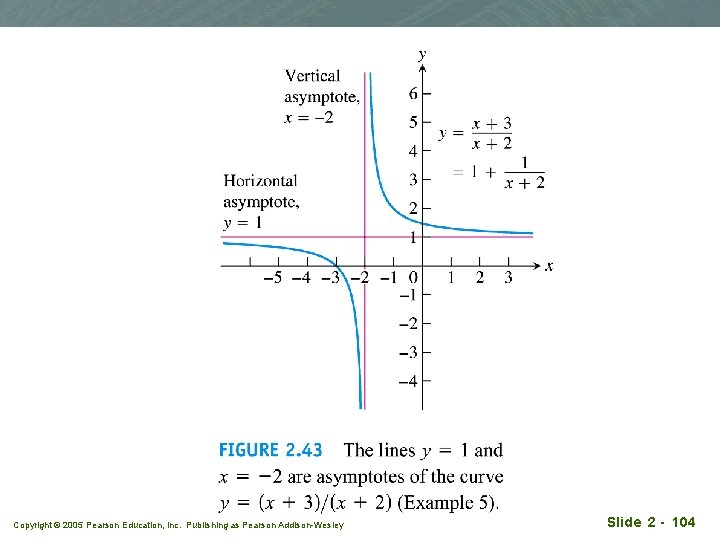
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 104

Asymptote need not be two-sided q Example 6 q Solution: Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 105
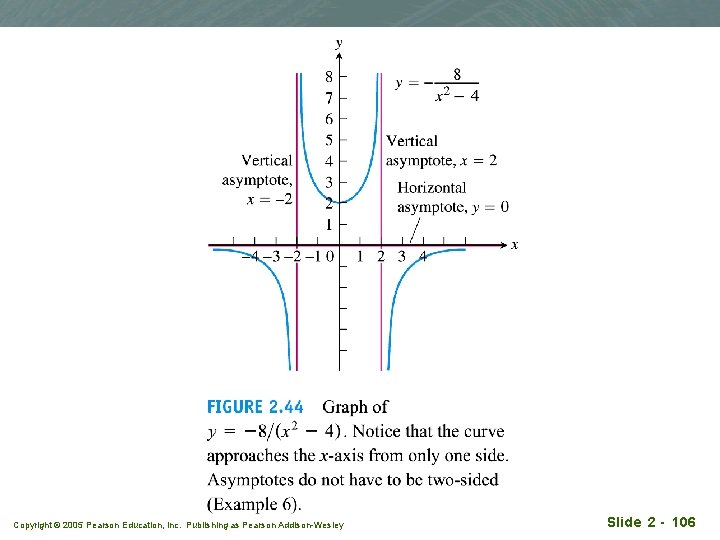
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 106

Example 8 q. A rational function with degree of freedom of numerator greater than degree of denominator q Solution: Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley linear remainder Slide 2 - 107
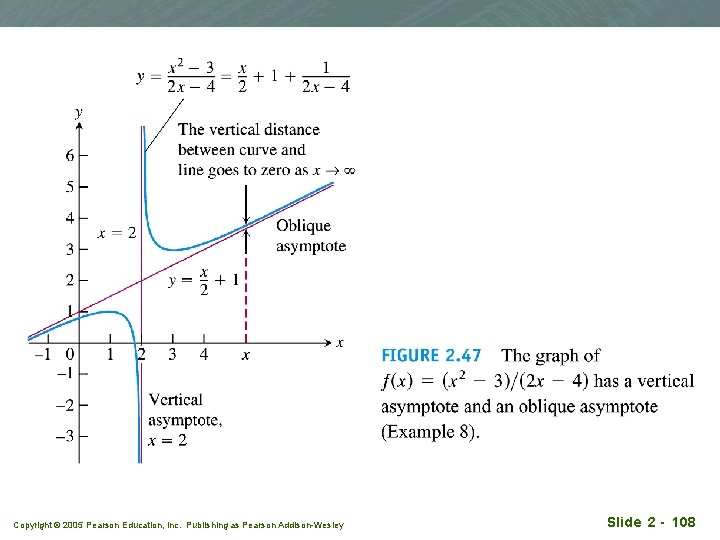
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 108

2. 6 Continuity Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 110

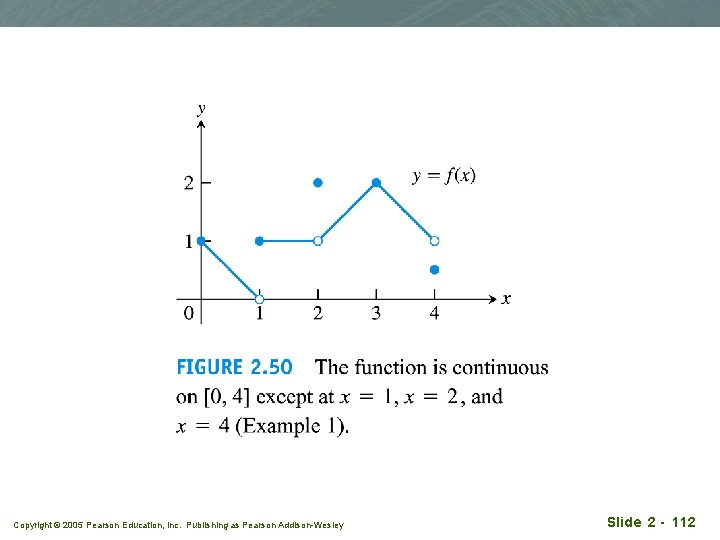
Continuity at a point q Example 1 q Find the points at which the function f in Figure 2. 50 is continuous and the points at which f is discontinuous. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 111
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 112

q q f continuous: At x = 0 At x = 3 At 0 < c < 4, c 1, 2 q q q Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley f discontinuous: At x = 1 At x = 2 At x = 4 0 > c, c > 4 Why? Slide 2 - 113

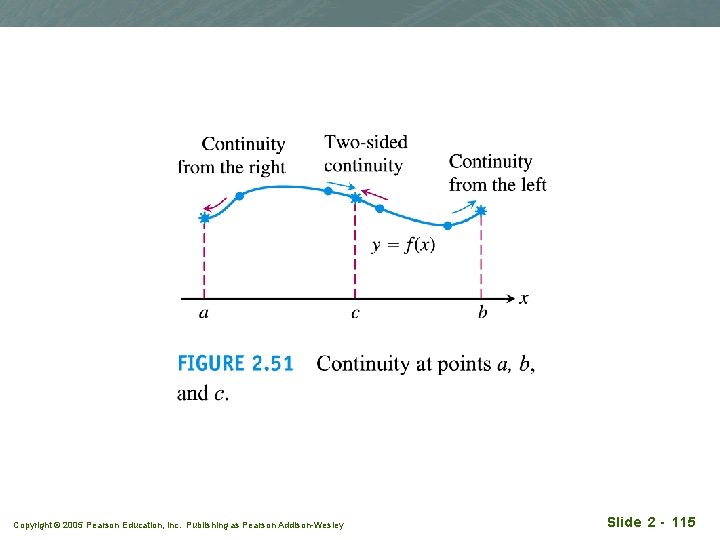
q To define the continuity at a point in a function's domain, we need to q define continuity at an interior point q define continuity at an endpoint Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 114
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 115

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 116

Example 2 q. A function continuous throughout its domain Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 117

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 118

Example 3 q The unit step function has a jump discontinuity Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 119

Summarize continuity at a point in the form of a test For one-sided continuity and continuity at an endpoint, the limits in parts 2 and parts 3 of the test should be replaced by the appropriate one-sided limits. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 120
![Example 4 q The greatest integer function q yx q The function is not Example 4 q The greatest integer function, q y=[x] q The function is not](https://slidetodoc.com/presentation_image_h2/367bf486312ac4dacea2b6bc6059a425/image-121.jpg)
Example 4 q The greatest integer function, q y=[x] q The function is not continuous at the integer points since limit does not exist there (left and right limits not agree) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 121
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 122

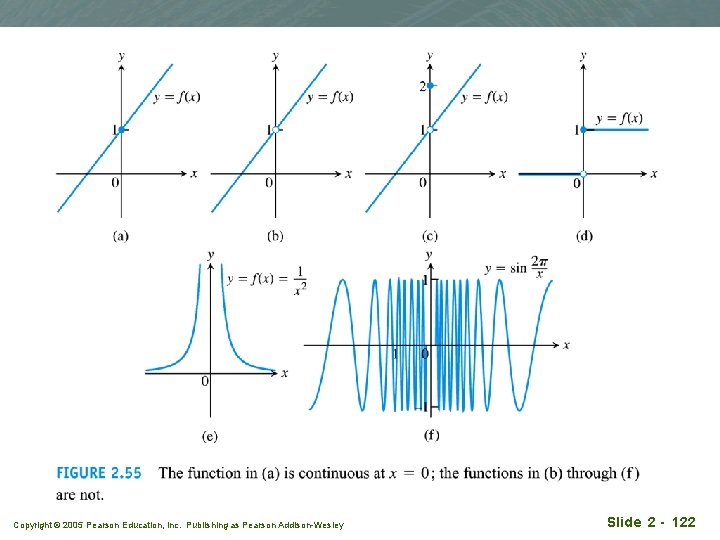
Discontinuity types q (b), (c) removable discontinuity q (d) jump discontinuity q (e) infinite discontinuity q (f) oscillating discontinuity Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 123

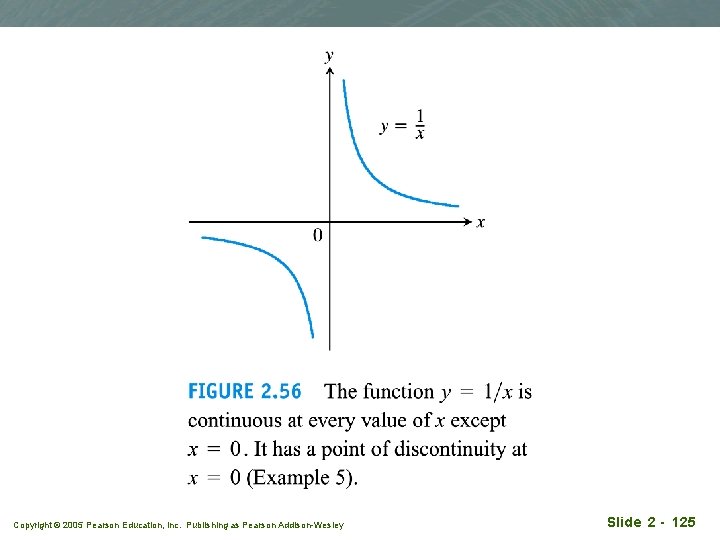
Continuous functions q. A function is continuous on an interval if and only if it is continuous at every point of the interval. q Example: Figure 2. 56 q 1/x not continuous on [-1, 1] but continuous over (-∞, 0) (0, ∞) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 124
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 125

Example 5 q Identifying continuous function q (a) f(x)=1/x q (b) f(x)= x q Ask: is 1/x continuous over its domain? Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 126

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 127

Example 6 q Polynomial and rational functions are continuous q (a) Every polynomial is continuous by q (i) q (ii) Theorem 9 q (b) If P(x) and Q(x) are polynomial, the rational function P(x)/Q(x) is continuous whenever it is defined. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 128

Example 7 q Continuity of the absolute function q f(x) = |x| is everywhere continuous q Continuity of the sinus and cosinus function q f(x) = cos x and sin x is everywhere continuous Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 129

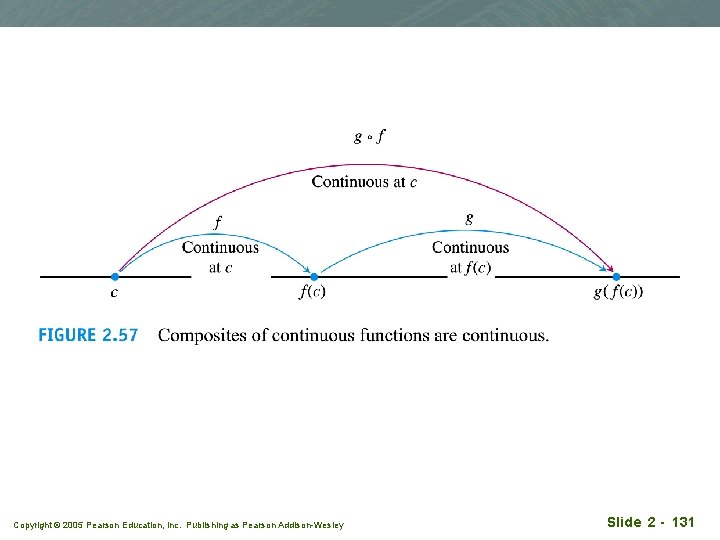
Composites q All composites of continuous functions are continuous Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 130
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 131

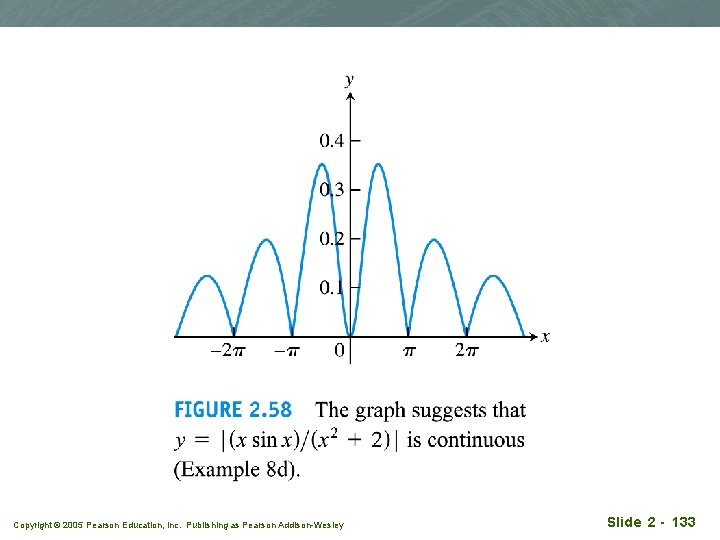
Example 8 q Applying Theorems 9 and 10 q Show that the following functions are continuous everywhere on their respective domains. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 132
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 133
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 134
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 135

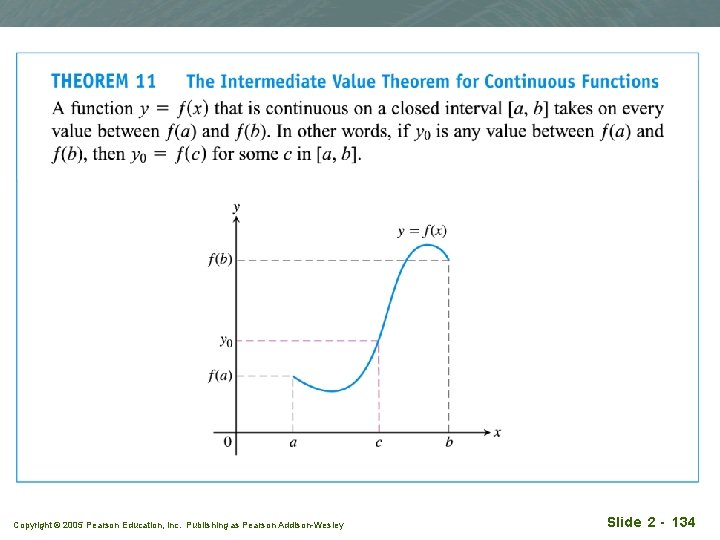
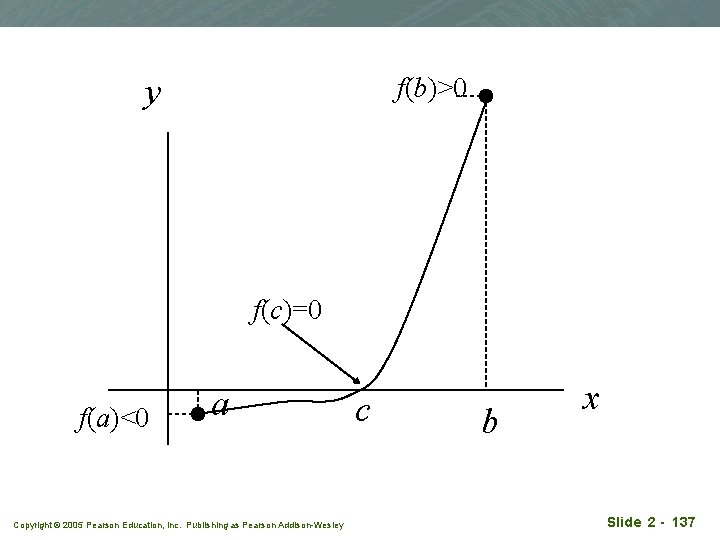
Consequence of root finding q q q A solution of the equation f(x)=0 is called a root. For example, f(x)= x 2 + x - 6, the roots are x=2, x= -3 since f(-3)=f(2)=0. Say f is continuous over some interval. Say a, b (with a < b) are in the domain of f, such that f(a) and f(b) have opposite signs. This means either f(a) < 0 < f(b) or f(b) < 0 < f(a) Then, as a consequence of theorem 11, there must exist at least a point c between a and b, i. e. a < c < b such that f(c)= 0. x=c is the root. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 136
f(b)>0 y f(c)=0 f(a)<0 a Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley c b x Slide 2 - 137

Example q q q q Consider the function f(x) = x - cos x Prove that there is at least one root for f(x) in the interval [0, p/2]. Solution f(x) is continuous on (-∞, ∞). Say a = 0, b = p/2. f(x=0) = -1; f(x = p/2) = p/2 f(a) and f(b) have opposite signs Then, as a consequence of theorem 11, there must exist at least a point c between a and b, i. e. a=0 < c < b= p/2 such that f(c)= 0. x=c is the root. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 138

2. 7 Tangents and Derivatives Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
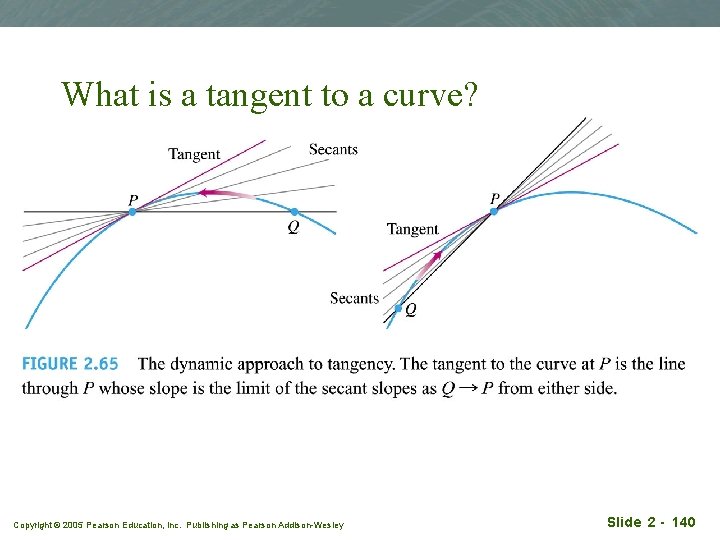
What is a tangent to a curve? Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 140

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 141
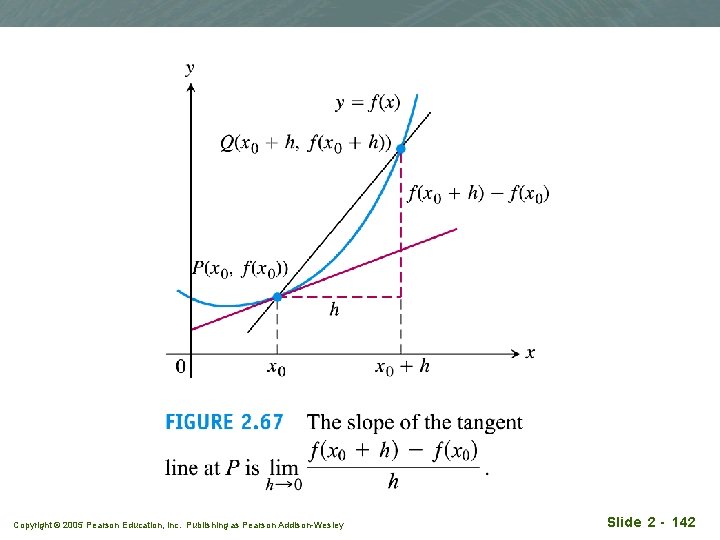
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 142

Example 1: Tangent to a parabola q Find the slope of the parabola y=x 2 at the point P(2, 4). Write an equation for the tangent to the parabola at this point. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 143

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 144
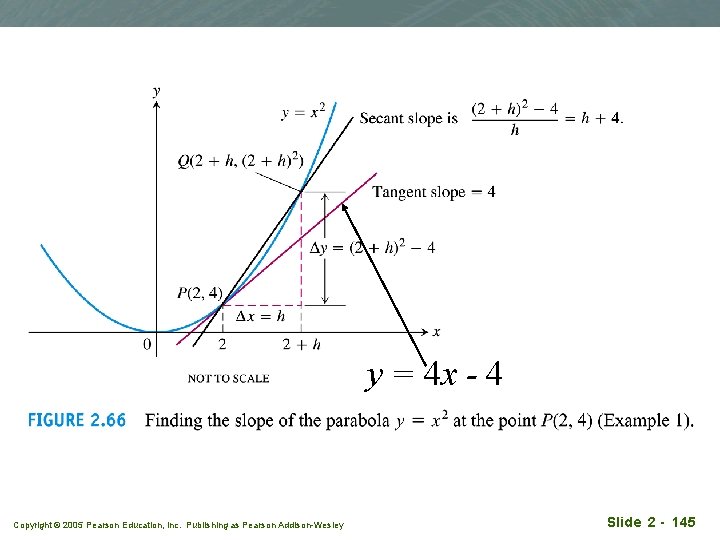
y = 4 x - 4 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 145

Example 3 q Slope and tangent to y=1/x, x 0 q (a) Find the slope of y=1/x at x = a 0 q (b) Where does the slope equal -1/4? q (c) What happens to the tangent of the curve at the point (a, 1/a) as a changes? Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 146
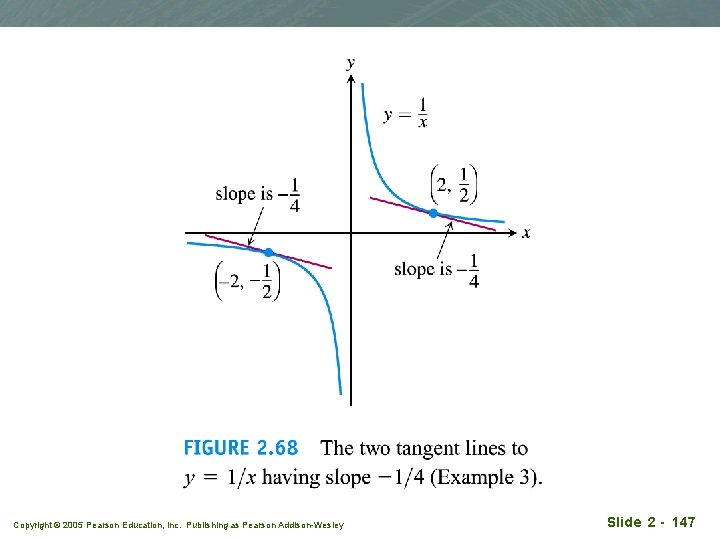
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 147
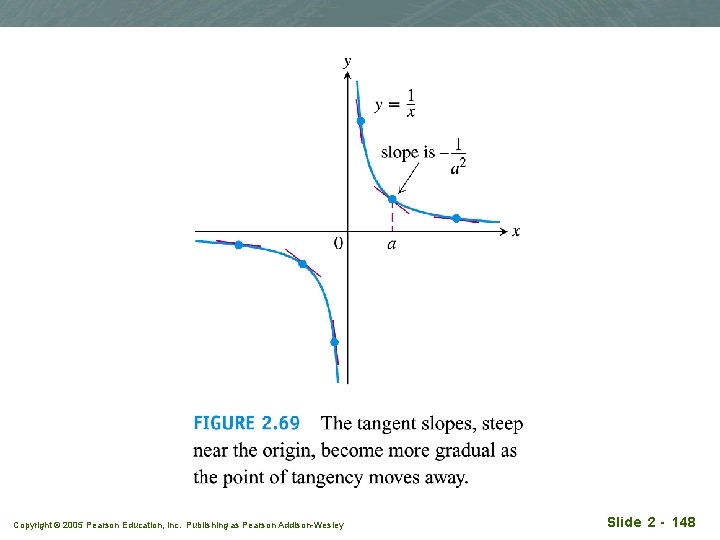
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 2 - 148
Source: https://slidetodoc.com/lecture-2-ch-2-limits-and-continuity-calculus/
0 Response to "Ch 2 Limits and Continuity Calculus"
Postar um comentário